Desconcertar a PISA

No es ningún secreto que los niños desfavorecidos tienen más probabilidades de luchar en la escuela. Durante décadas, la política pública se ha centrado en cómo reducir la brecha de rendimiento entre los estudiantes más pobres y los estudiantes más ricos. A pesar de los numerosos esfuerzos de reforma, estas brechas permanecen prácticamente sin cambios, un hecho que es profundamente frustrante y también un poco confuso. Sería razonable suponer que las desigualdades de fondo se reducirían con los años de escolaridad, pero eso no es lo que encontramos. A la edad de 18, más bien, encontramos diferencias que son aproximadamente del mismo tamaño que vemos a la edad de 6.

¿Significa esto que las escuelas no pueden abordar eficazmente la desigualdad? Ciertamente no. Uno de los factores clave que impulsan la desigualdad en las escuelas es la desigual oportunidad de aprender matemáticas (OTL). En artículos anteriores para Educador estadounidense y en otros lugares, definimos OTL como la relación importante pero a menudo pasada por alto entre el rendimiento matemático y la exposición al contenido matemático.*

Como explicaremos, es muy poco probable que los estudiantes aprendan material al que no están expuestos, y hay evidencia considerable de que los estudiantes desfavorecidos son sistemáticamente rastreados en aulas con contenido matemático más débil (por ejemplo, aritmética básica que se enseña en una clase llamada álgebra). ) En lugar de mitigar los efectos de la pobreza, muchas escuelas estadounidenses los están exacerbando.

El trabajo previo en esta área ha sido limitado por los datos disponibles,¹ pero el estudio más reciente del Programa de Evaluación Internacional de Estudiantes (PISA), coordinado por la Organización para la Cooperación y el Desarrollo Económico (OCDE), abre nuevas oportunidades para el análisis. El 2012 PISA incluye medidas de OTL de matemáticas a nivel de estudiante y proporciona evidencia poderosa de desigualdad en OTL y su relación con el rendimiento del estudiante. Específicamente, los últimos datos de PISA encuentran que:

• Hay una gran variación en la exposición al contenido matemático;
• OTL está fuertemente relacionado con el rendimiento del estudiante; y
• Los estudiantes de bajos ingresos generalmente están expuestos a matemáticas menos rigurosas.

No es solo que los estudiantes de bajos ingresos estén menos preparados cuando ingresan a la escuela; La debilidad de sus cursos de matemáticas en realidad les impide ponerse al día.
Lo realmente fascinante de los resultados de PISA es que este es un fenómeno global. En todos los países, una mayor exposición al contenido matemático formal se relacionó con un mejor rendimiento matemático, y casi todos los países mostraron una relación estadísticamente significativa entre los antecedentes socioeconómicos de los estudiantes y OTL. En otras palabras, el problema que identificamos en los Estados Unidos resulta ser un problema en todas partes.

Un hallazgo interesante de PISA fue que la mayor parte de la variación en el rendimiento de los estudiantes fue dentro de escuelas en lugar de entre ellos. Aquí en los Estados Unidos, estamos acostumbrados a hablar de "buenas escuelas" y "escuelas que no funcionan". Según PISA, esta perspectiva puede ser exagerada. En promedio, casi dos tercios de las diferencias en el rendimiento de los estudiantes en matemáticas se encuentran en la misma escuela, no en diferentes escuelas. Gran parte de esta diferencia reside entre las aulas, ya que los estudiantes en el mismo grado cubren contenido matemático profundamente diferente, incluso cuando sus clases comparten el mismo título del curso.² Estados Unidos se destaca, pero no como podría esperarse: aquí, más de las tres cuartas partes de las diferencias en el rendimiento de las matemáticas están dentro de la misma escuela. El problema parece ser menos escuelas desiguales que aulas desiguales.

Estos hallazgos deberían hacernos reconsiderar nuestro enfoque de la reforma educativa. La desigualdad educativa no es un problema específico de los Estados Unidos, pero algunos sistemas educativos hacen un trabajo mucho mejor que nosotros para hacer frente a los efectos de la pobreza. Más importante aún, el contenido matemático que se enseña en el aula desempeña un papel fundamental, un hecho que ha recibido muy poca atención y que examinamos aquí.

Disipando los mitos de PISA

PISA es una evaluación internacional que mide la alfabetización de los estudiantes de 15 en matemáticas, lectura y ciencias. Primero administrado en 2000, PISA se administra cada tres años. Los resultados de la evaluación más reciente, administrada a más de 500,000 a nivel mundial en 2012, se publicaron en diciembre de 2013. Las entidades gubernamentales participantes fueron los países 34 de la OCDE, incluidos los Estados Unidos, así como los países 28 no pertenecientes a la OCDE (y tres jurisdicciones en China: Hong Kong, Macao y Shanghai). Centramos este artículo en los resultados matemáticos PISA de los países 34 OECD.

Los resultados del último estudio de matemáticas de PISA fueron bastante similares a los de otras evaluaciones internacionales: el rendimiento de los estudiantes estadounidenses (481) fue en un grado estadísticamente significativo por debajo del promedio de otros países ricos de la OCDE (494) y sustancialmente detrás de la cima países de ejecución (como Corea del Sur en 554). A pesar de varias rondas de reforma educativa, la situación de los Estados Unidos está más o menos donde estaba hace casi dos décadas.

La respuesta a estos resultados ha sido familiar, y los defensores los interpretaron para que se ajustaran a sus ideas preconcebidas. Algunos sostienen que la continua mediocridad de los estudiantes estadounidenses de matemáticas es un problema grave que requiere una acción importante (que varía según la predisposición ideológica del hablante), mientras que otros explican estos hallazgos al sugerir que las comparaciones internacionales son injustas debido a la mayor diversidad de Estudiantes estadounidenses y / o el mayor compromiso de los Estados Unidos con el concepto de igualar las oportunidades educativas para todos los estudiantes.

También podemos esperar ver que uno de los países con mejor desempeño en PISA se convertirá en una especie de moda educativa, con decenas de artículos de periódicos y montones de documentos de política dedicados a comprender el secreto de su éxito, tal como lo han hecho las rondas anteriores de PISA. fue testigo de enamoramiento en serie con Japón, Singapur y Finlandia. Esto no quiere decir que no se haya aprendido nada de estos países, por supuesto.^†

Aunque ciertamente es comprensible, todas estas reacciones pierden el punto. Antes de profundizar en lo que PISA puede decirnos útilmente sobre el aprendizaje de las matemáticas en los Estados Unidos y cómo podemos mejorarlo, disipemos algunas ideas falsas. Primero está la creencia de que los puntajes de estudiantes de matemáticas de EE. UU. De débiles a medianos pueden explicarse por una diferencia en quién toma el examen. Es sorprendente la frecuencia con la que uno escucha la afirmación de que otros países solo permiten que sus estudiantes de élite tomen PISA, mientras que Estados Unidos se asegura de que los estudiantes de todos los niveles académicos sean evaluados.

La realidad es que todos los países de la OCDE que participan en PISA o, para el caso, TIMSS (el Estudio Internacional de Tendencias en Matemáticas y Ciencias, otra evaluación internacional destacada) deben cumplir requisitos muy estrictos en términos de participación de los estudiantes para ser incluidos. Los organizadores del estudio son extremadamente sensibles al problema del sesgo de la muestra. Sin ser demasiado técnico, PISA se administra a una muestra aleatoria de todas las escuelas de un país, y dentro de cada escuela de la muestra, a una muestra aleatoria de todos los niños de 15. Los investigadores que realizan PISA se aseguran de que los estudiantes que toman la prueba reflejen con precisión a toda la población de estudiantes de 15 de cada país.

Un malentendido común sobre la naturaleza de los puntajes de las pruebas internacionales a menudo resulta en un enfoque exclusivo en los resultados de la "carrera de caballos" de PISA: clasificar a las naciones por sus puntajes y tratar de discernir cuáles están bien y cuáles están mal. Hacer tales comparaciones es tentador y refleja nuestro interés similar en comparar el desempeño de los países en los Juegos Olímpicos y la Copa del Mundo. Pero las clasificaciones de país en PISA no son lo mismo que comparar registros de victorias y derrotas para equipos deportivos.

Como discutimos a continuación, la mayor parte de la variación en el rendimiento del estudiante es dentro de países, no entre países. Sí, los estudiantes ricos en Japón obtienen mejores resultados que los estudiantes ricos en Alemania, pero la brecha entre los estudiantes más ricos y los más pobres dentro de cualquier país es mucho mayor que la brecha entre países. Como resultado, comparar las variaciones entre países en lugar de las clasificaciones basadas en los puntajes de PISA podría ser la más útil de las comparaciones internacionales. La comparación de un grupo de países de alto rendimiento con otros en algunas métricas clave, como las brechas entre los estudiantes más ricos y los más pobres, para ver qué patrones generales surgen contribuye a una comprensión más profunda de los problemas educativos clave dentro de cada país y en todo el mundo.

También debemos resistir la tentación de suponer que el sistema educativo de los Estados Unidos no ha visto cambios en el puntaje en los últimos doce años. Aunque el ranking de matemáticas PISA de EE. UU. No ha cambiado esencialmente, hay signos de progreso. Por ejemplo, en el 2003 PISA, el rendimiento de los estudiantes de EE. UU. Fue estadísticamente significativo por debajo del promedio de la OCDE en las cuatro subescalas de contenido matemático: (1) cambio y relaciones, (2) espacio y forma, (3) cantidad, y (4) incertidumbre y datos.³ Nueve años más tarde, el rendimiento matemático de los estudiantes estadounidenses fue estadísticamente indistinguible del promedio de la OCDE en dos subescalas matemáticas: cambio y relaciones (que está estrechamente relacionado con el álgebra), e incertidumbre y datos (que está estrechamente relacionado con la probabilidad y las estadísticas). Esto representa un progreso notable si no espectacular. Aunque no podemos decir con certeza, el mejor desempeño de los Estados Unidos en álgebra puede estar relacionado con un mayor énfasis en los temas de álgebra en los estándares curriculares estatales de octavo grado a partir de hace una década.

Dicho esto, Estados Unidos todavía tiene un camino por recorrer para garantizar que todos los estudiantes estén expuestos al álgebra en octavo grado. Como hemos escrito anteriormente, dicha exposición los prepara para niveles más altos de matemáticas en la escuela secundaria y la educación postsecundaria. Según nuestra investigación, el álgebra y la geometría son temas que se enseñan en octavo grado en prácticamente todos los países que participan en TIMSS, pero en los Estados Unidos, existe una gran variabilidad en el contenido de matemáticas que los estudiantes aprenden en octavo grado. Hemos encontrado que, según los estándares internacionales, a nuestros estudiantes de octavo grado se les enseña demasiado a menudo el contenido de matemáticas de sexto grado.

Sin embargo, los Estándares Estatales Básicos Comunes en matemáticas nos dan la esperanza de que se parecen a los estándares de los países de alto rendimiento al exhibir las características clave de coherencia, rigor y enfoque. El énfasis que estos nuevos estándares ponen en el álgebra también es alentador. Por ejemplo, un dominio de operaciones y pensamiento algebraico para los grados de jardín de infantes a 5 sienta las bases para el álgebra en octavo grado.

Una mirada a PISA y TIMSS

Tal como lo vemos, un beneficio importante de PISA es que sus datos pueden usarse para sacar conclusiones tentativas sobre lo que influye en el aprendizaje de los estudiantes para bien o para mal. PISA nos muestra que lo que se les enseña a los estudiantes, el contenido de la instrucción matemática, influye de manera crítica en lo que los estudiantes saben. Igual de importante, revela que las oportunidades educativas relacionadas con la cobertura de ese contenido varían ampliamente en cada país, y que los estudiantes de entornos desfavorecidos están expuestos sistemáticamente a un contenido matemático más débil, lo que empeora la desigualdad educativa.

Lectores de nuestras piezas anteriores en Educador estadounidense podría estar pensando que todo esto suena familiar, y debería serlo. En esos artículos, escribimos sobre la oportunidad de aprender y sobre cómo las escuelas estadounidenses se caracterizan por la desigualdad generalizada en OTL, desigualdad que está fuertemente asociada con el contexto socioeconómico de los estudiantes.

Aunque explícito El seguimiento de los estudiantes de secundaria de EE. UU. en general ha disminuido, nuestros estudios indican que todavía es una práctica muy común pero a menudo pasada por alto.⁴ Con los resultados PISA más recientes, ahora tenemos razones para creer que el seguimiento no es solo un problema con las escuelas estadounidenses, sino también un problema global.

La base para estudiar OTL a nivel internacional se basa en TIMSS, que nos permitió identificar la fuerte relación de OTL con el aprendizaje de los estudiantes hace más de una docena de años.⁵ Pero hay limitaciones en cuanto a qué tan lejos podría llegar un análisis utilizando los datos de TIMSS. En TIMSS, la medida de OTL se basó en una encuesta de docentes en un pequeño número de aulas muestreadas al azar dentro de cada escuela. El PISA más nuevo, por el contrario, pide una muestra aleatoria de todos los estudiantes de una escuela y, por lo tanto, de múltiples aulas, sobre el contenido matemático al que habían estado expuestos, ya sea matemática formal, matemática aplicada o problemas de palabras.

Si bien las preguntas de PISA son menos extensas que las formuladas en TIMSS, PISA incluye preguntas sobre los antecedentes familiares de un estudiante, lo que permite el desarrollo de un índice del estado socioeconómico del estudiante (el índice educativo, social y cultural de PISA) capaz de aplicarse en todos los países. La ventaja de estas preguntas es que ahora podemos estudiar las desigualdades en OTL y los antecedentes socioeconómicos de los estudiantes, y la relación entre ellos, de una manera mucho más detallada, una que represente más plenamente la diversidad en la escolarización dentro de los países.

Otra distinción entre PISA y TIMSS está en cómo definen la idea de oportunidad para aprender. En el TIMSS original (1995), OTL se definió como (1) exposición a temas de matemáticas y (2) la cantidad de tiempo que los maestros dedicaron a esos temas. En el último estudio de PISA, OTL se identifica como familiaridad y exposición a un pequeño conjunto de temas matemáticos clave (al igual que la lista de temas que se encuentran en TIMSS), así como aplicaciones del mundo real y problemas de palabras. Los temas de matemáticas son principalmente los que se encuentran típicamente en los grados 8 a 12 que definen el contenido académico del currículo de secundaria inferior y superior. La OCDE etiqueta esta "matemática formal".⁶ Mientras que TIMSS evalúa el conocimiento matemático formal (incluidos los conceptos, habilidades, algoritmos y habilidades de resolución de problemas típicamente cubiertos en las escuelas), PISA evalúa la alfabetización matemática, que la OCDE define como "la capacidad de un individuo para formular, emplear e interpretar matemáticas en una variedad de contextos Incluye razonamiento matemático y el uso de conceptos matemáticos, procedimientos, hechos y herramientas para describir, explicar y predecir fenómenos. Ayuda a las personas a reconocer el papel que juegan las matemáticas en el mundo y a emitir los juicios y decisiones bien fundados que necesitan los ciudadanos constructivos, comprometidos y reflexivos ".

La relación de OTL con el rendimiento

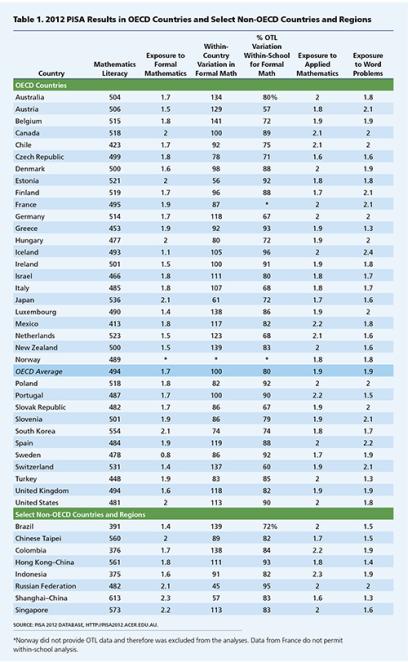
Primero, usamos PISA para examinar cómo la exposición a las matemáticas formales, las matemáticas aplicadas y los problemas de palabras se relaciona con la alfabetización matemática (ver la Tabla 1 a continuación). Una comparación de los promedios de los países para estas tres variables OTL revela una variación considerable entre países en el énfasis puesto en cada uno, medido en una escala 0 a 3. Entre las naciones 33 OECD que participaron en el estudio de OTL (Noruega no recopiló datos OTL, mientras que los datos de Francia no permiten el análisis OTL dentro de la escuela), Japón y Corea del Sur tuvieron el promedio más alto de matemáticas formales (2.1) y Suecia el más bajo (0.8). Portugal y México promediaron 2.2 en matemáticas aplicadas en comparación con el 1.6 de la República Checa, mientras que Turquía y Grecia pusieron el menor énfasis en los problemas de palabras (1.3) e Islandia en la mayoría (2.4). Una comparación entre países sugiere que los sistemas educativos que dedicaron la mayor parte del tiempo a las matemáticas aplicadas tienden a tener puntajes promedio PISA más bajos, una relación que es estadísticamente significativa.

^{(Haga clic en la imagen para ampliarla)}

Sin embargo, como mencionamos anteriormente, la clasificación de los países puede ser bastante engañosa. Por ejemplo, surge una historia diferente cuando nos enfocamos en los patrones dentro de los países de la OCDE Encontramos eso dentro de países, las tres medidas de oportunidad de aprender —matemáticas formales, matemáticas aplicadas y problemas de palabras— tenían una relación positiva estadísticamente significativa con el rendimiento de los estudiantes.⁷ En otras palabras, cuando los estudiantes tenían más oportunidades de estudiar matemática formal, matemática aplicada y problemas de palabras, su desempeño en PISA tendía a aumentar, sin importar en qué país vivía ese estudiante.

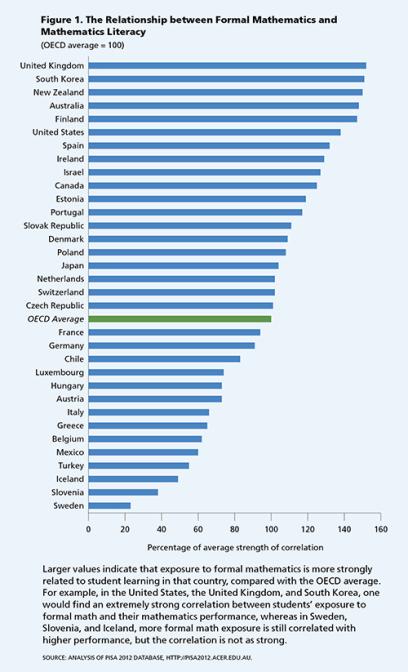
La exposición a problemas de palabras tuvo una pequeña asociación positiva con los puntajes de PISA, mientras que las matemáticas formales tuvieron una relación positiva muy fuerte, con un tamaño de efecto promedio estimado que fue alrededor de la mitad de una desviación estándar. Para los Estados Unidos, la relación de las matemáticas formales con el rendimiento es particularmente fuerte, alrededor de dos tercios de una desviación estándar (ver Figura 1 a continuación). En resumen, PISA sugiere fuertemente la importancia del contenido matemático formal.

^{(Haga clic en la imagen para ampliarla)}

El efecto de las matemáticas aplicadas fue más complicado. Las matemáticas aplicadas se asociaron con un mayor rendimiento hasta cierto punto, después de lo cual una exposición adicional a las matemáticas aplicadas tuvo una relación negativa. En general, entre los países de la OCDE, el aumento de la ausencia de exposición a la exposición moderada se asoció con un aumento sustancial en el rendimiento de los estudiantes (que se aproxima a la mitad de una desviación estándar), más allá del cual hay ganancias limitadas o incluso caídas en el rendimiento con una exposición más frecuente. En otras palabras, después de cierto punto, más trabajo en la aplicación de las matemáticas en realidad está relacionado con niveles más bajos de alfabetización matemática.

La pequeña relación positiva de los problemas de palabras y la relación positiva (pero más complicada) de las matemáticas aplicadas se mantuvo en muchos de los países PISA. Sin embargo, la relación positiva de las matemáticas formales con los resultados de los estudiantes fue mucho más poderosa y mucho más consistente, manteniéndose en todos los sistemas educativos (países y regiones de la OCDE y no miembros de la OCDE que participaron en PISA).

Una razón para la relación más fuerte de exposición con las matemáticas formales podría ser que los estudiantes deben sentirse muy cómodos con un concepto matemático antes de poder aplicarlo de manera significativa. Por ejemplo, para calcular qué porcentaje de los ingresos va a pagar por la vivienda o el cuidado de los niños, o cualquier otro gasto importante, una persona debe tener una comprensión clara de cómo funcionan las proporciones. Parece que una base sólida en los conceptos matemáticos formales es un requisito previo tanto para comprender como para usar las matemáticas.

Todo lo que esto implica es que si bien el contenido matemático en problemas de palabras o en contextos del mundo real puede mejorar el rendimiento de los estudiantes, lo más crucial es el contenido de la instrucción matemática en sí.

Variación en la oportunidad de aprender

Anteriormente, notamos la gran variación en el rendimiento matemático dentro de los países de la OCDE. También existe una tremenda variación en la exposición al contenido matemático formal (como se muestra en la columna "Variación dentro del país en matemática formal" de la Tabla 1), que va desde Bélgica (porcentaje 41 por encima de la variación promedio de la OCDE) hasta Estonia (porcentaje 44 por debajo del promedio de la OCDE variación). A medida que exploramos con más detalle a continuación, Estados Unidos está un 13 por ciento por encima de la variación promedio de la OCDE. PISA demuestra de manera bastante convincente que algunos países hacen un trabajo mucho mejor que otros al asegurarse de que todos sus estudiantes tengan un acceso más o menos igual al contenido matemático riguroso, que incluye las matemáticas formales.

Esto nos lleva al problema de la desigualdad educativa. La educación ha sido vista tradicionalmente como una forma de establecer un "campo de juego nivelado" entre los niños de diferentes orígenes.⁸ La esperanza ha sido que el acceso a buenas escuelas asegurará la igualdad de oportunidades, de modo que el mérito personal en lugar del ingreso familiar determinará el curso de la vida. Esta visión ha jugado un papel fundamental en la autocomprensión de los Estados Unidos.

Sin embargo, los resultados de PISA confirman un creciente cuerpo de investigación que indica que el sistema educativo de EE. UU. No está cumpliendo con las responsabilidades que le hemos asignado, no porque los estudiantes, los padres y los maestros no estén haciendo lo mejor posible, sino porque la educación El sistema no ha logrado garantizar la igualdad de oportunidades educativas. No solo los puntajes de los estudiantes varían enormemente, sino que también lo hace la exposición al contenido formal de matemáticas. Además, este es un problema en todas partes, no solo en los Estados Unidos. Y tristemente, aunque algunos países son mejores en la distribución más equitativa de oportunidades para aprender matemáticas, ninguno de ellos ha logrado eliminar estas inequidades por completo.

Los estudiantes de bajos ingresos están expuestos a contenido más débil

Estas desigualdades educativas están de hecho fuertemente asociadas con el estatus socioeconómico de los estudiantes. Idealmente, esperamos que los estudiantes de bajos ingresos reciban al menos las mismas oportunidades educativas, si no mayores, para ponerse al día con sus compañeros. En cambio, en En todos los países participantes en PISA, los estudiantes más pobres recibieron un contenido matemático más débil. Los sistemas escolares en todo el mundo no están mejorando las desigualdades de fondo; Los están empeorando. Nuestro análisis de los datos de PISA sugiere que la exposición a las matemáticas formales es al menos tan importante como la formación de los estudiantes en la construcción de la alfabetización matemática de los estudiantes. Teóricamente, OTL podría usarse para mitigar los efectos de la pobreza estudiantil; en cambio, encontramos lo contrario.

La gravedad de la desigualdad educativa varía apreciablemente de un país a otro, ya sea comparando variaciones en OTL o la influencia del estatus socioeconómico de los estudiantes para diferentes países. También hay una gran diferencia en cómo los sistemas educativos, ya sea por diseño o por consecuencia, contribuyen a estas desigualdades. Por ejemplo, en algunos países, las desigualdades entre las escuelas son mayores que en otras (Austria tiene más variación entre las escuelas que, por ejemplo, Islandia). También hay brechas sustanciales en la oportunidad de aprender entre escuelas de altos y bajos ingresos, con las brechas más pequeñas entre los sistemas de la OCDE en Estonia y las brechas más grandes en Austria. Estas desigualdades están relacionadas con el rendimiento promedio del país: los sistemas con mayores diferencias entre escuelas (definidas por un nivel socioeconómico alto versus bajo de estudiantes) en OTL también tienen mayores diferencias entre escuelas en alfabetización matemática.⁹

Es vital recordar que, en cada país, la mayor parte de la variación en las oportunidades educativas es dentro de escuelas, no entre ellos. En promedio, aproximadamente el 80 por ciento de la variación en OTL entre los países de la OCDE está dentro de las escuelas (ver Tabla 1). El hecho de que la mayoría de las desigualdades en el contenido matemático se encuentre dentro de las escuelas sugiere que los intentos de reducir la desigualdad educativa que se enfoca en las escuelas de alto y bajo rendimiento tendrán efectos limitados.

Una mirada más detallada a los Estados Unidos

Aunque, según muchas métricas, Estados Unidos es bastante similar a otros países, hay algunas áreas en las que se destaca (y no para mejor). Estados Unidos parece tener una mayor desigualdad en la exposición al contenido matemático que otros sistemas educativos. Tiene una variación total 13 por ciento mayor en OTL de matemáticas formales que el promedio de la OCDE, la variación 12 más grande entre los sistemas 33 OECD. Como podríamos esperar, la mayor variación en OTL entre los estudiantes de EE. UU. Se asocia con una relación superior a la media entre la exposición a las matemáticas formales y la alfabetización matemática (una mayor exposición aumenta la alfabetización matemática), donde Estados Unidos ocupa el sexto lugar entre los países de la OCDE. Las desigualdades en la enseñanza de las matemáticas, por lo tanto, juegan un papel más importante en la contabilización de la desigualdad educativa en los Estados Unidos que en otras naciones.

Lo más notable es el hallazgo contraintuitivo de que Estados Unidos se caracteriza por una menor desigualdad entre escuelas que otros países. Durante años, la discusión sobre la desigualdad educativa y su asociación con la pobreza estudiantil se ha concentrado en el problema de las "escuelas que no funcionan", lo que implica que la mayoría de las desigualdades en el sistema educativo estadounidense son producto de las diferencias entre las escuelas. Esta creencia puede haber llevado a algunos a suponer que los problemas en el sistema educativo de los Estados Unidos son aislados, fallas locales y no una falla del sistema educativo en general. Aunque es el caso de que los estudiantes de EE. UU. En las escuelas con estudiantes más desfavorecidos están expuestos a un contenido matemático más débil que los estudiantes en las escuelas más ricas, esta es una menores problema en los Estados Unidos de lo que es en otros sistemas educativos.

Sin embargo, los datos de PISA revelan que la desigualdad entre escuelas en el rendimiento de los estudiantes y las oportunidades de los estudiantes se ve eclipsada por la desigualdad dentro de la escuela. Las tres cuartas partes (76 por ciento) de la variación en el rendimiento de los estudiantes son en realidad dentro de la escuela (en comparación con un promedio de la OCDE de 64 por ciento), y el 90 por ciento de la variación en la oportunidad de aprender matemáticas formales es dentro de la escuela (en comparación con un promedio de la OCDE de 80 por ciento). Estas cifras ubican a los Estados Unidos entre las naciones con la mayor proporción de desigualdad dentro de la escuela: séptimo entre los países de la OCDE por desigualdad OTL y 10 por desigualdad en los resultados de los estudiantes.

Otra característica de los Estados Unidos que puede diferenciarlo de otros países es el carácter descentralizado de la escolarización estadounidense. Mientras que otras naciones tienen sistemas federales, Estados Unidos se ha destacado por su estructura educativa extremadamente fragmentada.¹⁰ Esta descentralización de la estructura educativa ha estado acompañada de una gran variación en los estándares educativos en todos los estados, así como de grandes diferencias en el contenido de la enseñanza de las matemáticas en las escuelas, incluso en el mismo estado.¹¹

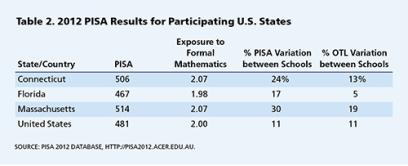
Sin embargo, durante las últimas décadas, los gobiernos estatales asumieron una parte cada vez mayor de la responsabilidad de las finanzas escolares, la administración y el plan de estudios. Estados Unidos no es un gran sistema educativo, sino (como mínimo) 50 autónomo. Sabemos por la Evaluación Nacional del Progreso Educativo (NAEP), realizada por el Centro Nacional de Estadísticas de Educación del Departamento de Educación de los EE. UU., Que al igual que existe una variación considerable entre los países, también existe una variación entre los estados de los EE. UU. Uno de los frutos del PISA más reciente es que tres estados, Connecticut, Florida y Massachusetts, acordaron participar en el estudio con muestras estadísticas completas (en lugar de agruparse con estudiantes de otros estados). Esto significa que podemos tratarlos como sistemas independientes (o "países") con el fin de compararlos con el promedio de los EE. UU. Y con los sistemas educativos de otros países (consulte la Tabla 2 a continuación).

^{(Haga clic en la imagen para ampliarla)}

Lo que encontramos es que, si bien algunas características interesantes distinguen estos estados entre sí y de otros sistemas, comparten la mayoría de los mismos patrones generales que encontramos en el resto del mundo. Confirmando los resultados de NAEP, Massachusetts tiene puntajes promedio más altos que el resto de los Estados Unidos (514 vs. 481), aunque no se encuentra entre los de mejor desempeño en PISA.

Para los tres estados, la mayor parte de la variación en el rendimiento de los estudiantes y la oportunidad de aprender es dentro de las escuelas, y no entre ellas, y OTL está en un grado estadísticamente significativo relacionado con los resultados de los estudiantes, incluso controlando los antecedentes socioeconómicos del estudiante. En cada uno de estos tres estados, emerge el mismo patrón básico que encontramos en los Estados Unidos en su conjunto y en otros países: las desigualdades en matemáticas formales OTL exacerban las desigualdades socioeconómicas. Al analizar las diferencias entre los estudiantes de bajos y altos ingresos (definidos por el promedio de los EE. UU.), Encontramos grandes brechas tanto en la oportunidad de aprender como en los puntajes de PISA, ya sea analizados entre escuelas, dentro de las escuelas o una combinación de ambos.

Nuestros análisis indicaron que aunque las relaciones dentro de la escuela son aún más importantes, los factores a nivel escolar juegan un papel mucho más importante en Massachusetts que en los otros dos estados. Por ejemplo, el porcentaje 30 de la variación en los puntajes PISA y el porcentaje 19 de la variación en OTL fueron atribuibles a factores a nivel escolar. Estos hallazgos son solo sugerentes, pero apuntan a algunas vías valiosas para la exploración. Por ejemplo, ¿qué tiene el sistema educativo de Massachusetts que le da mayor importancia a las escuelas? ¿Y qué características del gobierno educativo de Florida han resultado en una menor desigualdad?

Además, debemos tener precaución al comparar las unidades subnacionales con las nacionales. En este momento, Shanghai está recibiendo mucha atención debido a sus altos puntajes de PISA, pero Shanghai no es toda China más de lo que Massachusetts representa a todo Estados Unidos. Tampoco se sigue necesariamente que los estados o ciudades hayan alcanzado su estatus debido a prácticas o políticas educativas. Por ejemplo, los puntajes cercanos de PISA de la región italiana de Lombardía (517) y Massachusetts (514) pueden reflejar en parte sus similitudes demográficas, en particular su riqueza relativa.

* * *

Un análisis cuidadoso de los datos de PISA puede decirnos mucho más que qué país se encuentra actualmente en la cima de la clasificación internacional. La investigación basada en PISA presenta una fuerte evidencia de que Estados Unidos pone en desventaja sistemáticamente a los estudiantes de bajos ingresos al privarlos de un contenido matemático sólido, pero también nos dice que este es un fenómeno global. En la mayoría de los aspectos, Estados Unidos no es tan diferente de otros países.

PISA también incluye algunas sorpresas reales que deberían incitarnos a reexaminar nuestro enfoque de la reforma educativa. Aunque confirma la gran importancia del contenido de la instrucción, PISA nos advierte que con respecto a la inclusión de aplicaciones del mundo real, más no es necesariamente mejor. Con ese fin, no debemos concentrarnos demasiado en tales aplicaciones a expensas de enseñar contenido matemático. También pone en duda la idea de que el seguimiento ha disminuido en las escuelas estadounidenses.

Sin embargo, PISA proporciona razones para el optimismo. La fuerte relación entre la oportunidad de aprender y los resultados de los estudiantes sugiere que las escuelas realmente importan. Algunos sistemas educativos son mucho más efectivos para minimizar la desigualdad educativa, un hecho que, en los Estados Unidos, debería inspirar admiración y un compromiso renovado con el desafío de la reforma educativa al servicio de la calidad y la igualdad.

William H. Schmidt es Profesor Distinguido de la Universidad, codirector del Centro de Políticas Educativas, y el investigador principal principal del proyecto de Promoción de resultados rigurosos en educación matemática y científica en la Universidad Estatal de Michigan. Es miembro de la Academia Nacional de Educación y miembro de la Asociación Americana de Investigación Educativa. Nathan A. Burroughs es investigador asociado del Centro para el Estudio del Currículo de la Universidad Estatal de Michigan. Partes de este artículo aparecieron en dos publicaciones en el blog del Instituto Albert Shanker: "PISA y TIMSS: una distinción sin diferencia? ”En diciembre 4, 2014; y "La relación global entre el contenido del aula y los resultados educativos desiguales"En julio 29, 2014.

*Ver "Igualdad de oportunidades educativas"En la edición Winter 2010 – 2011 de Educador estadounidense y "Saltando a la vida"En la edición Spring 2013. (volver al articulo)

^†Para obtener más información sobre lo que Estados Unidos puede aprender de Finlandia, Singapur y Japón, consulte "Una lección modelo"En la edición Spring 2012 de Educador estadounidense, Más allá de los libros de texto de matemáticas de Singapur"En la edición Winter 2009 – 2010, y"Creciendo juntos"En la edición Fall 2009. (volver al articulo)

Notas finales

1 El Estudio Internacional de Tendencias en Matemáticas y Ciencias (TIMSS) analiza el conocimiento de los estudiantes y la exposición al contenido de matemáticas en los niveles de país, escuela y aula, pero no proporciona información a nivel de estudiante.

2 William H. Schmidt, Curtis C. McKnight, Richard T. Houang, HsingChi Wang, David E. Wiley, Leland S. Cogan y Richard G. Wolfe, Por qué las escuelas importan: una comparación transnacional de currículo y aprendizaje (San Francisco: Jossey-Bass, 2001).

3 Se puede encontrar una descripción de las cuatro subescalas de contenido en Organización para la Cooperación y el Desarrollo Económico, Resultados PISA 2012vol. 1 Lo que los estudiantes saben y pueden hacer: rendimiento del estudiante en matemáticas, lectura y ciencias (París: OCDE, 2014). Cambio y relaciones: esta categoría enfatiza "las relaciones entre objetos y los procesos matemáticos asociados con los cambios en esas relaciones" (95). Espacio y forma: esta categoría enfatiza “las relaciones espaciales entre objetos, y la medición y otros aspectos geométricos del mundo espacial” (103). Cantidad: Esta categoría enfatiza "comparaciones y cálculos basados ​​en relaciones cuantitativas y propiedades numéricas de objetos y fenómenos" (105). Incertidumbre y datos: esta categoría enfatiza “interpretar y trabajar con datos y con diferentes formas de presentación de datos, y problemas que involucran razonamiento probabilístico” (105).

4 William Schmidt y Curtis McKnight, Desigualdad para todos: el desafío de la desigualdad de oportunidades en las escuelas estadounidenses (Nueva York: Teachers College Press, 2012).

5 Schmidt y col. Por qué son importantes las escuelas.

6 De William H. Schmidt, Pablo Zoido y Leland Cogan, "Schooling Matters: Opportunity to Learn in PISA 2012" Documentos de trabajo de educación de la OCDE, No. 95 (París: OCDE, 2013), 7: “Se desarrollaron tres índices a partir de los ítems del cuestionario del estudiante: matemáticas formales, un indicador del grado de exposición del estudiante a los temas de álgebra y geometría en la instrucción en el aula; problemas de palabras, un indicador de la frecuencia con que los estudiantes encontraron problemas de palabras en sus estudios de matemáticas; y las matemáticas aplicadas, un indicador de la frecuencia en que los estudiantes en sus clases de matemáticas encontraron problemas que requerían la aplicación de las matemáticas, ya sea en una situación matemática o en un contexto cotidiano del mundo real ".

7 Los análisis dentro del país se realizaron con un modelo jerárquico en los niveles entre y dentro de la escuela. Se encontraron los siguientes tipos de relaciones en ambos niveles, pero aquí informamos sobre los resultados dentro de la escuela donde estaba presente la mayor parte de la variación en OTL y rendimiento. Cuando se hace referencia al "promedio", esto se refiere solo a los países de la OCDE.

8 Schmidt y McKnight, Desigualdad para todos.

9 Schmidt, Zoido y Cogan, "Schooling Matters".

10 William H. Schmidt, Curtis C. McKnight y Senta A. Raizen, Una visión dividida: una investigación de la educación en ciencias y matemáticas de los EE. UU. (Dordrecht, Países Bajos: Kluwer Academic Publishers, 1997).

11 Schmidt y McKnight, Desigualdad para todos.