ETodo el mundo quiere que los maestros estén bien informados. Sin embargo, hay poco acuerdo sobre exactamente qué tipos de conocimiento son más importantes para los maestros. ¿Deben los maestros tener un conocimiento profundo de la materia que están enseñando, obtenida de estudios universitarios, cursos de posgrado adicionales o incluso experiencia en investigación? ¿Necesitan entender cómo suelen pensar los estudiantes cuando abordan un problema o una teoría? ¿Existe alguna combinación óptima de estos diferentes tipos de conocimiento?
Los investigadores han especulado durante mucho tiempo que el conocimiento de un maestro sobre conceptos erróneos comunes de los estudiantes podría ser crucial para el aprendizaje de los estudiantes.1 Esta visión reconoce que el aprendizaje se trata tanto de desaprender viejas ideas como de aprender nuevas.2 A los alumnos a menudo les resulta difícil cambiar sus conceptos erróneos, ya que estas son ideas que tienen sentido para ellos. Algunos investigadores defienden, por lo tanto, que los maestros deben conocer conceptos erróneos comunes de los estudiantes sobre los temas que enseñan,3 y otros sugieren que los profesores se entrevisten4 o prueba5 sus alumnos para revelar preconceptos de los alumnos al principio del proceso de aprendizaje. Sin embargo, la investigación no llega a evaluar el conocimiento de los maestros sobre conceptos erróneos particulares de los estudiantes y el impacto real de este conocimiento en el aprendizaje de los estudiantes.
Las discusiones como estas, si usan datos, a menudo se basan en métodos indirectos para medir el conocimiento del maestro. Los títulos universitarios obtenidos, los cursos tomados y las calificaciones obtenidas a menudo sirven como representantes del conocimiento de la materia de un maestro, que se identifica como la comprensión conceptual general de un área de materia que posee un maestro.6 Pero los estudios que investigan rigurosamente la relación entre los diferentes tipos de conocimiento del maestro y los logros de los estudiantes en la comprensión son raros.7
Nos propusimos comprender mejor la relación entre el conocimiento del profesor de ciencias, específicamente, y el aprendizaje de los estudiantes.8 Administramos ítems de evaluación de opción múltiple idénticos tanto a los maestros de ciencias físicas de la escuela intermedia (que cubre temas básicos en física y química) como a sus estudiantes durante todo el año escolar. Muchas de las preguntas requerían una elección entre conceptos científicos aceptados y conceptos erróneos comunes que han sido bien documentados en la literatura de educación científica.9 También les pedimos a los maestros que identificaran qué respuesta incorrecta creían que los estudiantes tenían más probabilidades de seleccionar como correcta. A través de una prueba posterior de los estudiantes al final del año escolar, pudimos estudiar el impacto en el aprendizaje de los estudiantes sobre el conocimiento de las ciencias por parte de los maestros y la precisión de sus predicciones sobre dónde es probable que los estudiantes tengan ideas erróneas.
No todos los ítems tenían respuestas incorrectas muy populares, pero para aquellos que sí (ítems 12 del 20, o 60 por ciento), encontramos que los maestros que podían identificar estos conceptos erróneos tenían mayores logros en el aula, mucho más que si los maestros supieran solo lo correcto respuestas Este hallazgo sugiere que la capacidad de un maestro para identificar la respuesta incorrecta más común de los estudiantes en elementos de opción múltiple, una forma de conocimiento del contenido pedagógico, es una medida adicional de la efectividad del maestro de ciencias. Para los ítems en los cuales los estudiantes generalmente no tenían ideas erróneas populares, el conocimiento de la materia del maestro solo representaba mayores ganancias de los estudiantes.
Nuestro estudio
El objetivo de nuestro estudio fue probar dos hipótesis con respecto al conocimiento del maestro en los cursos de ciencias físicas de la escuela intermedia:
Hipótesis 1: El conocimiento de los maestros sobre un concepto de ciencia particular que están enseñando predice las ganancias de los estudiantes en ese concepto.
Hipótesis 2: El conocimiento de los maestros sobre los conceptos erróneos comunes de los estudiantes relacionados con un concepto de ciencia particular que están enseñando predice las ganancias de los estudiantes en ese concepto.
Evaluamos el conocimiento de la materia de los maestros y su conocimiento de los conceptos erróneos de los estudiantes en el contexto de los conceptos clave definidos por los Estándares Nacionales de Educación en Ciencias del National Research Council (NRC) y medimos su relación con el aprendizaje de los estudiantes.* Administramos los mismos elementos de opción múltiple tanto para estudiantes como para maestros. Y les pedimos a los maestros que identificaran el ítem incorrecto (es decir, el concepto erróneo del alumno) que creían que los alumnos elegirían con mayor frecuencia en lugar de la respuesta correcta. Este método nos permitió evaluar simultáneamente el conocimiento de los maestros sobre la materia y los conceptos erróneos de los estudiantes y examinar si estas medidas del maestro predicen las ganancias de los estudiantes en las aulas de ciencias físicas de la escuela intermedia.
Los estudiantes de ciencias a menudo luchan con conceptos erróneos, y las pruebas de opción múltiple funcionan bien en el diagnóstico de conceptos erróneos populares que pueden impedir el aprendizaje de conceptos de ciencias.10 Buenos ejemplos incluyen las causas de las estaciones y de las fases de la luna. Por ejemplo, una visión particularmente común, a menudo sostenida por adultos, es que las estaciones son causadas por la órbita elíptica de la tierra en lugar del ángulo cambiante de los rayos del sol que golpean la superficie de la tierra. En el documental Un universo privado, estudiantes de último año universitarios graduados brillantes y articulados, algunos con especialización en ciencias, revelaron sus malentendidos sobre temas de ciencias comunes en la escuela intermedia.11 Si los maestros tienen esos conceptos erróneos ellos mismos o simplemente no son conscientes de que sus alumnos tienen tales ideas, sus intentos de enseñar conceptos importantes pueden verse comprometidos.
Medimos las ganancias en los conceptos clave durante un curso de ciencias físicas de la escuela intermedia de un año. Como es común en este tipo de investigación, controlamos las diferencias en la demografía de los estudiantes, como la raza, el origen étnico, el idioma hablado en el hogar y la educación de los padres. Mediante el uso de ítems de prueba individuales, podríamos evaluar cuán fuertemente se asociaron el conocimiento de la materia de los maestros y el conocimiento de los conceptos erróneos de los estudiantes con las ganancias de los estudiantes.
El diseño de nuestro estudio también fue capaz de explicar la cantidad de contenido de ciencias físicas que se enseñó durante los años de la escuela intermedia, que puede variar mucho. Mientras que algunas escuelas dedican un año académico completo al tema, otras escuelas incluyen ciencias físicas dentro de una secuencia de ciencias generales que cubre las ciencias de la tierra y el espacio y las ciencias de la vida. Además, nos preocupaba que el logro científico inicial de las aulas participantes pudiera ocultar cualquier cambio en el rendimiento estudiantil durante el año escolar. Por ejemplo, puede ser que, en comparación con sus colegas menos experimentados, a los maestros más experimentados o expertos se les asignaron estudiantes que han demostrado un mayor rendimiento previo. La administración de una prueba previa, una prueba de mitad de año y una prueba posterior nos permitió controlar el nivel de conocimiento básico de los estudiantes.
Nuestro esfuerzo inicial de reclutamiento a nivel nacional arrojó maestros 620 de ciencias físicas de séptimo y octavo grado en las escuelas 589 (el porcentaje de 91 era público). De los maestros que al principio se ofrecieron como voluntarios para formar parte de este estudio, 219 siguió adelante. Tenían bastante experiencia, con un tiempo medio de enseñanza de los años 15.6 y un tiempo medio enseñando ciencias físicas de la escuela intermedia de los años 10.4. Tenían una variedad de preparación de pregrado: 17 por ciento tenía un título en ciencias físicas; 25 por ciento, un título en otra ciencia; 36 por ciento, un título en educación científica; 23 por ciento, un título de educación en un área que no sea ciencia; y 9 por ciento, un título en otro campo. El 8 por ciento de los maestros tenía múltiples títulos universitarios. Del total de la muestra, 56 por ciento tenía un título de posgrado en educación y 14 por ciento tenía un título de posgrado en ciencias.
A cambio de su participación, ofrecimos informar a los maestros los puntajes agregados de sus alumnos y las ganancias asociadas de los alumnos en comparación con nuestra muestra nacional.12 El setenta y ocho por ciento de los estudiantes estaban en octavo grado, mientras que 22 estaba en séptimo grado. Al final, obtuvimos datos utilizables de un total de estudiantes 9,556 de maestros 181.
Detalles de diseño
Para la evaluación, construimos preguntas de opción múltiple13 que reflejan los estándares de contenido de ciencias físicas del NRC para los grados 5 – 8.14 Si bien estamos obligados a publicar la redacción real de las preguntas de 20 porque la evaluación es ampliamente utilizada por los programas de desarrollo profesional a nivel nacional,15 la evaluación aborda tres áreas de contenido: propiedades y cambios de propiedades en la materia (seis preguntas), movimientos y fuerzas (cinco preguntas) y transferencia de energía (nueve preguntas). (Consulte la Tabla 1 para más detalles).
Las preguntas de opción múltiple se clasificaron en dos categorías con respecto a la popularidad relativa de las respuestas incorrectas. Ocho de las preguntas de 20 tenían conceptos erróneos "débiles" o no evidentes, con la respuesta incorrecta más común elegida por menos de la mitad de los estudiantes que dieron respuestas incorrectas. Considere los resultados para el elemento de muestra 1 (que se muestra a continuación), por ejemplo. Mientras que el 38 por ciento de los estudiantes respondió esta pregunta correctamente (opción d), el correspondiente 62 por ciento respondió incorrectamente, con 42 por ciento de aquellos que fueron incorrectos seleccionando la opción b. Si bien la opción b fue la respuesta incorrecta más popular, no fue elegida por más de la mitad de los estudiantes que respondieron incorrectamente, por lo que se considera que el ítem no tiene un concepto erróneo identificable.
1 Un científico está haciendo experimentos con mercurio. Calienta un poco de mercurio hasta que se convierte en gas. ¿Con cuál de los siguientes está más de acuerdo?
Un total de preguntas de 12 tenían conceptos erróneos "fuertes", lo que significa que 50 por ciento o más de los estudiantes que eligieron una respuesta incorrecta prefirieron un distractor en particular. Por ejemplo, como se muestra en el ítem de muestra 2, solo el 17 por ciento de los estudiantes respondió la pregunta correctamente (opción a), y el porcentaje correspondiente de 83 respondió incorrectamente. Una fracción muy grande (59 por ciento) de estudiantes eligió una respuesta incorrecta en particular, la opción d; de los estudiantes que eligieron una respuesta incorrecta, 71 por ciento prefirió este solo distractor. Esta respuesta indica una fuerte idea errónea.
2 Eric está mirando una vela encendida con mucho cuidado. Después de que toda la vela se haya quemado, se pregunta qué pasó con la cera. Él tiene una serie de ideas; ¿con cuál estás más de acuerdo?
La cobertura en el aula del contenido representado por los elementos de prueba fue casi universal. Solo ocho maestros informaron que no cubrieron el contenido probado por un elemento en particular, y dos maestros informaron que no cubrieron el contenido en dos elementos.
En la Tabla 1, desglosamos por estándar los conceptos generales abordados por los ítems de la prueba 20, con sus conceptos erróneos comunes señalados en cursiva debajo de cada uno. Los estudios anteriores relevantes sobre estos conceptos erróneos específicos de los estudiantes se citan en las notas finales.
En las evaluaciones de mitad de año y de fin de año, incluimos cuatro preguntas no científicas, dos de lectura y dos de matemáticas, para tener una idea general del compromiso y el esfuerzo de los estudiantes en las pruebas mismas. Las dos preguntas de lectura fueron construidas para representar la comprensión de los estudiantes de un texto relacionado con la ciencia. El primero de ellos requería que los estudiantes comprendieran el texto real, mientras que el segundo requería que dedujeran del texto. De manera similar, de las dos preguntas de matemáticas, una requirió una operación aritmética bien definida, mientras que la segunda requirió que los estudiantes identificaran las características relevantes de un problema de palabras antes de responder. Los puntajes promedio en lectura y matemáticas fueron ambos 58 por ciento.
Estos cuatro elementos se usaron para construir lo que se llama una variable compuesta. Los estudiantes que respondieron correctamente a menos de la mitad de los elementos de contenido no relacionados con la ciencia (27 por ciento de los participantes) fueron etiquetados como "bajo nivel de no conocimiento"; aquellos que respondieron correctamente al menos el 50 por ciento de los cuatro ítems de lectura y matemática fueron etiquetados como "no científicos". Este índice nos permitió examinar las ganancias para cada grupo por separado. Presumimos que los estudiantes que se desempeñaron en el rango bajo de no ciencia en lectura y matemática simple habrían tenido dificultades para responder las preguntas de ciencias en el examen o simplemente no habrían dado su mejor esfuerzo.
Conocimiento de la materia del maestro y conocimiento de los conceptos erróneos de los estudiantes
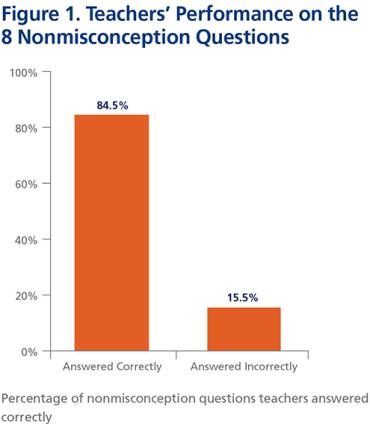
El desempeño de los docentes en el conocimiento de la materia en la prueba preliminar fue relativamente sólido, con un porcentaje de 84.5 correcto en los elementos que no son de concepción y un porcentaje de 82.5 en los elementos de concepción incorrecta. En promedio, los maestros se perdieron tres de los artículos de 20. El conocimiento de los maestros sobre los conceptos erróneos de los estudiantes, es decir, la capacidad de identificar la respuesta incorrecta más común en los ítems erróneos, fue débil, con un puntaje promedio de 42.7 por ciento identificado. En promedio, identificaron solo cinco de los artículos de 12 con fuertes conceptos erróneos.
El desempeño de los docentes en cada uno de los ocho ítems no erróneos se clasificó en una de dos categorías (ver Figura 1 a continuación):
- Conocimiento de la materia (el maestro respondió correctamente): 84.5 porcentaje de respuestas.
- Sin conocimiento de la materia (el maestro respondió incorrectamente): 15.5 por ciento de las respuestas.
(Haga clic en la imagen para ampliarla)
Como se esperaba, la mayoría de los maestros eran competentes en su conocimiento de la materia, especialmente cuando el ítem no incluía un concepto erróneo fuerte entre sus distractores.
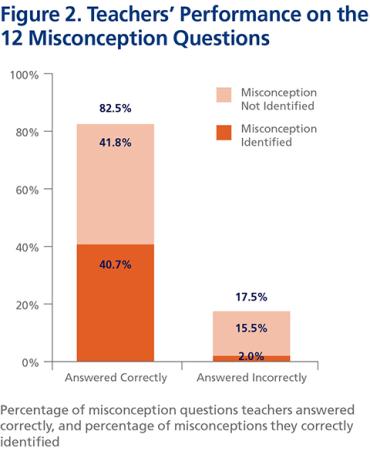
El desempeño de los docentes en cada uno de los conceptos erróneos de 12 se clasificó en una de las cuatro categorías posibles (consulte la Figura 2 a continuación):
- Tenía tanto conocimiento de la materia como conocimiento de los conceptos erróneos de los estudiantes (el maestro respondió correctamente y sabía la respuesta incorrecta más común de los estudiantes): 40.7 por ciento de las respuestas.
- Tenía conocimiento de la materia, pero no conocía los conceptos erróneos de los estudiantes (el maestro respondió correctamente pero no sabía la respuesta incorrecta más común de los estudiantes): 41.8 porcentaje de respuestas.
- No tenía conocimiento de la materia, pero tenía conocimiento de los conceptos erróneos de los estudiantes (el maestro respondió incorrectamente pero sabía la respuesta incorrecta más común de los estudiantes): 2.0 porcentaje de respuestas.
- No tenía conocimiento de la materia ni conocimiento de los conceptos erróneos de los estudiantes (el maestro respondió incorrectamente y no sabía la respuesta incorrecta más común de los estudiantes): 15.5 por ciento de las respuestas.
(Haga clic en la imagen para ampliarla)
En el caso de los maestros que no conocen la ciencia (es decir, que responden el ítem incorrectamente), la mayoría seleccionó el concepto erróneo dominante del estudiante como su propia respuesta "correcta". Decidimos combinar las categorías tercera y cuarta en una, porque los maestros en ambas categorías no poseían el conocimiento relevante de la materia para ese ítem. Además, es difícil interpretar el significado de la categoría muy pequeña (2 por ciento) de las respuestas de los maestros que carecían de conocimiento de la materia pero mostraron conocimiento de los conceptos erróneos de los estudiantes.
El conocimiento de la materia del maestro y el conocimiento de los conceptos erróneos de los estudiantes, por lo tanto, parecen relacionados, en lugar de ser independientes entre sí.25 Mientras que algunos investigadores han argumentado que no hay diferencias formales entre los tipos de conocimiento del maestro,26 parece que el conocimiento de la materia, al menos en la forma que medimos, debe considerarse una condición previa necesaria, pero no suficiente, del conocimiento de los conceptos erróneos de los estudiantes.
Logro estudiantil
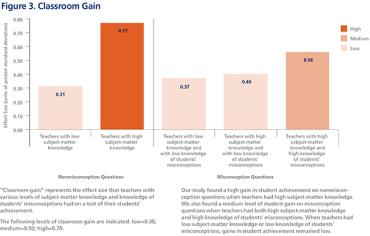
Los puntajes de los estudiantes fueron relativamente bajos, lo que indica que los ítems de evaluación de ciencias fueron difíciles. La puntuación media previa a la prueba en todos los ítems (tanto los que no tienen conceptos erróneos como los que tienen conceptos erróneos) fue 37.7 por ciento. Las puntuaciones medias en la prueba final fueron más altas en 42.9 por ciento: 44.8 por ciento para los ítems sin conceptos erróneos y 41.7 por ciento para aquellos con conceptos erróneos. A los estudiantes les resultó un poco más fácil aprender el contenido para el cual no parecía haber una idea errónea dominante. Nuestro análisis del conocimiento de los maestros al comienzo del año muestra altos niveles de conocimiento de la materia, con algunas debilidades y niveles bastante moderados de conocimiento de los conceptos erróneos de los estudiantes, medidos por la predicción de los maestros de las respuestas incorrectas más comunes de sus estudiantes. . Lo más importante, encontramos que las ganancias de los estudiantes están relacionadas con el conocimiento del maestro, como se muestra a continuación en la Figura 3. Los estudiantes obtuvieron grandes ganancias en preguntas que no eran de concepción cuando los maestros tenían un alto conocimiento de la materia. En preguntas erróneas, los estudiantes obtuvieron ganancias medias si los maestros tenían ambas alto conocimiento de la materia y alto conocimiento de conceptos erróneos. En todas las demás constelaciones, las ganancias de los estudiantes fueron bajas.
(Haga clic en la imagen para ampliarla)
Además, encontramos diferencias interesantes entre los estudiantes con poca o poca ciencia. El primero mostró ganancias mucho mayores que el segundo. Los estudiantes con alto nivel de ciencia, incluso si su maestro no tenía el conocimiento requerido de la materia y el conocimiento de los conceptos erróneos de los estudiantes, obtuvieron ganancias moderadas. Hay muchas explicaciones posibles para este resultado. Por ejemplo, estos estudiantes pueden haber encontrado formas de obtener conocimiento de otras fuentes, como sus libros de texto, tareas o discusiones con otros estudiantes.
Tener un maestro con más conocimientos se asocia con ganancias aún mayores para los estudiantes de alto nivel de ciencia que para los de bajo nivel de ciencia, recordando el llamado efecto Matthew, que, en términos generales, dice que aquellos con un atributo en abundancia (en en este caso, el conocimiento) tiende a ganar más que los que comienzan con menos.27 La investigación ha encontrado que los estudiantes con bajos niveles de lectura exhiben ganancias más bajas en otras materias porque gran parte del esfuerzo detrás del aprendizaje requiere leer textos.28
También puede darse el caso de que los estudiantes que respondieron incorrectamente los ítems de lectura y matemáticas incrustados simplemente no hayan tomado en serio estas preguntas (o la prueba en su conjunto). Aquellos con puntajes bajos en estas preguntas pueden haber entendido mal estas preguntas porque no estaban interesados, y su desempeño en los ítems científicos de 20 también podría haber sufrido. Si este es el caso, los hallazgos para estudiantes de altos niveles no científicos (73 por ciento del total) deben enfatizarse como un reflejo más equitativo del impacto del conocimiento de la materia del maestro y el conocimiento de los conceptos erróneos de los estudiantes.
Sin embargo, se observó una ganancia significativa en los ítems que no son de concepción para los estudiantes con poca ciencia si tenían un maestro con conocimientos, por lo que al menos algunos parecen haber tomado las pruebas en serio. También parece que los estudiantes con bajos puntajes de lectura y matemática eran particularmente dependientes del conocimiento de la materia del maestro, sin exhibir ganancias significativas a menos que sus maestros tuvieran el conocimiento de la materia requerido para estos elementos (y los elementos no tenían conceptos erróneos). La falta de ganancia en los conceptos erróneos para estos estudiantes, independientemente del nivel de conocimiento de la materia del maestro o el conocimiento de los conceptos erróneos de los estudiantes, es particularmente preocupante. Es posible que estos artículos simplemente se hayan leído mal, o que sean cognitivamente demasiado sofisticados para estos estudiantes, o que los estudiantes no hayan hecho todo lo posible en una prueba de bajo riesgo.
Entre los estudiantes con altos puntajes en matemáticas y lectura, nuestro análisis revela una relación clara entre el conocimiento del maestro y las ganancias de los estudiantes. Para los ítems que no son de concepción, las ganancias de los estudiantes son casi el doble si el maestro sabe la respuesta correcta. Cuando los ítems tienen un concepto erróneo fuerte, es probable que los estudiantes cuyos maestros tengan conocimiento de los conceptos erróneos de los estudiantes ganen más que los estudiantes de maestros que carecen de este conocimiento. Gran parte de lo que sucede en muchas aulas de ciencias podría considerarse simplemente como una demostración del conocimiento de la materia del profesor, sin tener en cuenta el conocimiento de la materia del alumno. Sin el conocimiento de los maestros de conceptos erróneos relevantes para un concepto de ciencia en particular, parece que el éxito de sus estudiantes en el aprendizaje será limitado.
En particular, la "transferencia" del conocimiento de los maestros sobre la materia o el conocimiento de los conceptos erróneos de los estudiantes entre los conceptos parece ser limitada. Por ejemplo, la comprensión firme de un maestro de los circuitos eléctricos y los conceptos erróneos relevantes parece tener poco que ver con la enseñanza efectiva de las reacciones químicas. Los maestros que generalmente están bien versados en ciencias físicas aún pueden tener agujeros que afectan el aprendizaje de los estudiantes de un concepto particular. Nuestros hallazgos sugieren que es importante examinar el conocimiento del maestro en torno a conceptos particulares, porque el desempeño del estudiante a nivel de ítem está asociado con el conocimiento del maestro de un concepto particular.
Además, en los conceptos de enseñanza para los cuales los estudiantes tienen conceptos erróneos, el conocimiento de las ideas de los estudiantes puede ser el componente crítico que les permite a los maestros construir lecciones efectivas. Debido a que el conocimiento de los maestros sobre los conceptos erróneos de los estudiantes es bajo, en comparación con su conocimiento del contenido de ciencias, el desarrollo profesional centrado en esta área podría ayudar sustancialmente a los maestros (y estudiantes).
Smateria súbita
El conocimiento es un importante predictor del aprendizaje de los estudiantes. La necesidad de que los maestros conozcan los conceptos que enseñan puede parecer una verdad. Pero si bien se puede suponer que el contenido de ciencia de la ciencia física de la escuela intermedia es, en general, bien entendido por los maestros, existen agujeros notables en su conocimiento, que difieren según el maestro. No es sorprendente que los maestros con el conocimiento apropiado de la materia de un concepto dado puedan lograr mayores ganancias con sus estudiantes que aquellos que carecen de ese conocimiento; un maestro sin conocimiento de la materia puede enseñar el concepto incorrectamente, y los estudiantes pueden terminar con la misma creencia incorrecta que su maestro.
La efectividad de los maestros de ciencias de la escuela intermedia puede tener más que ver con el dominio de todos los conceptos que enseñan que con la profundidad de sus conocimientos en cualquier tema en particular. La participación cada vez mayor de los profesores de ciencias en el desarrollo profesional de los docentes podría enfocar esos programas de manera demasiado limitada en las áreas especiales de especialización de los científicos, lo que podría aumentar el conocimiento de los temas de los participantes solo en un conjunto limitado de temas. Llevar a cabo una identificación diagnóstica y remediar los "agujeros" de conocimiento de los docentes podría resultar más ventajoso.
Un hallazgo intrigante de este estudio es que los maestros que conocen los conceptos erróneos más comunes de sus estudiantes tienen más probabilidades de aumentar el conocimiento científico de sus estudiantes que los maestros que no lo hacen. Tener un maestro que solo conoce la "verdad" científica parece ser insuficiente. Es mejor si un maestro también tiene un modelo de cómo los estudiantes tienden a aprender un concepto particular, especialmente si una creencia común puede dificultar la aceptación de la visión científica o el modelo.
Este hallazgo también tiene implicaciones prácticas. En el desarrollo profesional, un énfasis en aumentar el conocimiento de la materia por parte de los maestros sin prestar suficiente atención a los modelos mentales preconcebidos de los estudiantes de secundaria (así como también a los de los maestros) puede ser ineficaz para mejorar en última instancia el conocimiento de las ciencias físicas de sus estudiantes.
Philip M. Sadler es el director del Departamento de Educación Científica del Centro Harvard-Smithsoniano de Astrofísica. Su investigación se centra en evaluar las ideas erróneas científicas de los estudiantes; la transición de la escuela secundaria a la universidad de estudiantes que siguen carreras de ciencia, tecnología, ingeniería y matemáticas (STEM); y mejorar las habilidades de los profesores de ciencias. Gerhard Sonnert es investigador asociado en el Centro Harvard-Smithsoniano de Astrofísica. Su investigación se centra en el género en la ciencia, la sociología e historia de la ciencia y la educación científica. Este artículo está adaptado de Philip M. Sadler, Gerhard Sonnert, Harold P. Coyle, Nancy Cook-Smith y Jaimie L. Miller, "La influencia del conocimiento de los maestros sobre el aprendizaje de los estudiantes en las aulas de ciencias físicas de la escuela intermedia". Revista de investigación educativa estadounidense 50 (2013): 1020 – 1049. Copyright © 2013 por la American Educational Research Association. Publicado con permiso de SAGE Publications, Inc.
*Llevamos a cabo nuestro estudio antes de la llegada de los Estándares de Ciencias de la Próxima Generación, para los cuales los currículos aún no están ampliamente disponibles. (volver al articulo)
Notas finales
1 David P. Ausubel, Joseph D. Novak y Helen Hanesian, Psicología educativa: una visión cognitiva, 2nd ed. (Nueva York: Holt, Rinehart y Winston, 1978).
2 Lee S. Shulman, "Aquellos que entienden: el crecimiento del conocimiento en la enseñanza" Investigador Educativo 15, no. 2 (1986): 4 – 14. Otros dos estudios clave que enfatizan la importancia de la enseñanza temática y el conocimiento de las luchas y errores comunes de los estudiantes son Heather C. Hill, Stephen G. Schilling y Deborah Loewenberg Ball, "Desarrollando medidas del conocimiento matemático de los maestros para la enseñanza". Diario de la escuela primaria 105 (2004): 11 – 30; y Pamela L. Grossman, The Making of a Teacher: Teacher Knowledge and Teacher Education (Nueva York: Teachers College Press, 1990).
3 William S. Carlsen, "Dominios del conocimiento del maestro", en Examen del conocimiento del contenido pedagógico: el constructo y sus implicaciones para la educación científicaed. Julie Gess-Newsome y Norman G. Lederman (Boston: Kluwer Academic, 1999), 133 – 144; y John Loughran, Amanda Berry y Pamela Mulhall, Comprensión y desarrollo del conocimiento del contenido pedagógico de los docentes de ciencias, 2nd ed. (Rotterdam: Sense Publishers, 2012).
4 Eleanor Ruth Duckworth, "El tener ideas maravillosas" y otros ensayos sobre enseñanza y aprendizaje (Nueva York: Teachers College Press, 1987).
5 David Treagust, "Evaluación de conceptos erróneos de los estudiantes mediante elementos de diagnóstico de opción múltiple" Investigación en educación científica 16 (1986): 199 – 207.
6 Shulman, "Los que entienden".
7 Jürgen Baumert, Mareike Kunter, Werner Blum, et al., "Conocimientos matemáticos de los docentes, activación cognitiva en el aula y progreso del alumno" Revista de investigación educativa estadounidense 47 (2010): 133 – 180.
8 Nuestros esfuerzos fueron parte de un proyecto financiado por la National Science Foundation para producir un conjunto de evaluaciones con fines de diagnóstico en las aulas de la escuela intermedia que enseñan ciencias físicas (otorga EHR-0454631, EHR-0412382 y EHR-0926272). Las opiniones, hallazgos, conclusiones o recomendaciones expresadas en este material son de los autores y no reflejan necesariamente los puntos de vista de la National Science Foundation.
9 Philip M. Sadler, "Modelos psicométricos de las concepciones de los estudiantes en ciencias: conciliación de los estudios cualitativos y los instrumentos de evaluación basados en distractores" Revista de Investigación en Enseñanza de las Ciencias 35 (1998): 265 – 296; Kenneth J. Schoon, "Conceptos erróneos en las ciencias de la Tierra y el espacio: un estudio de edades cruzadas" (PhD diss., Loyola University of Chicago, 1989); y Treagust, "Evaluación de conceptos erróneos de los estudiantes".
10 Sadler, "Modelos psicométricos"; y Treagust, "Evaluación de conceptos erróneos de los estudiantes".
11 Centro Harvard-Smithsoniano de Astrofísica, Un universo privado, dirigida por Matthew H. Schneps y Philip M. Sadler (South Burlington, VT: Annenberg / CPB Project, 1987), videocasete VHS.
12 Algunas advertencias están en orden. Nuestras medidas de conocimiento de la materia del maestro y el conocimiento de los conceptos erróneos de los estudiantes pueden ser sustitutos de otras variables no incluidas. Uno podría imaginar, por ejemplo, que años de experiencia docente es el contribuyente clave para el conocimiento de la materia y el conocimiento de los conceptos erróneos de los estudiantes y, por lo tanto, las ganancias de los estudiantes. Para explorar si este podría ser el caso, investigamos modelos usando variables como los años de enseñanza de los maestros en el aula y los años de enseñanza de ciencias físicas, entre otros. Ninguno alcanzó un nivel de significación estadística cuando se incluyó con medidas de conocimiento de la materia y conocimiento de conceptos erróneos de los estudiantes. Otra consideración es que debido a que los maestros participantes se ofrecieron como voluntarios para unirse a este proyecto, nuestros resultados pueden no ser generalizables para otros maestros de ciencias físicas de la escuela intermedia. Puede ser que nuestros maestros confiaran más en sus habilidades o estuvieran ansiosos por participar porque sentían que sus estudiantes se desempeñarían bien. Además, nuestra muestra de estudiantes no es totalmente representativa de la población nacional: los estudiantes negros e hispanos están subrepresentados, y los estudiantes con padres que tienen títulos universitarios están sobrerrepresentados. Sin embargo, la muestra fue lo suficientemente grande como para haber capturado el rango de variación existente en las variables relevantes estudiadas, de modo que estos factores podrían controlarse en un modelo estadístico jerárquico.
13 Para una descripción del proceso utilizado para crear elementos e instrumentos de evaluación en todos los campos de la ciencia, vea Philip M. Sadler, Harold Coyle, Jaimie L. Miller, Nancy Cook-Smith, Mary Dussault y Roy R. Gould, "La astronomía e Inventario del concepto de ciencia espacial: desarrollo y validación de instrumentos de evaluación alineados con los Estándares Nacionales de Ciencia K – 12 ” Revisión de Educación Astronómica 8 (2010): 1 – 26.
14 Nuestras descripciones de las normas del Consejo Nacional de Investigación están adaptadas de la Academia Nacional de Ciencias, Estándares Nacionales de Educación Científica (Washington, DC: National Academy Press, 1996), 154 – 155.
15 Evaluaciones comparables están disponibles en línea en www.cfa.harvard.edu/smgphp/mosart.
16 BR Andersson, "Algunos aspectos de la comprensión de los niños sobre el punto de ebullición", en Investigación del desarrollo cognitivo en ciencias y matemáticas: actas de un seminario internacionaled. WF Archenhold y col. (Leeds, Reino Unido: Universidad de Leeds, 1980), 252 – 259.
17 Saouma B. BouJaoude, "Un estudio de la naturaleza de las comprensiones de los estudiantes sobre el concepto de quema," Revista de Investigación en Enseñanza de las Ciencias 28 (1991): 689 – 704.
18 Rosalind Driver, "Más allá de las apariencias: la conservación de la materia bajo transformaciones físicas y químicas", en Ideas infantiles en la cienciaed. Rosalind Driver, Edith Guesne y Andrée Tiberghien (Milton Keynes, Reino Unido: Open University Press, 1985), 145 – 169.
19 Ichio Mori, Masao Kojima y Tsutomu Deno, "Un niño forma el concepto de velocidad" Enseñanza de las ciencias 60 (1976): 521 – 529.
20 Lillian C. McDermott, Mark L. Rosenquist y Emily H. van Zee, "Dificultades de los estudiantes para conectar gráficos y física: ejemplos de cinemática" Revista estadounidense de física 55 (1987): 503 – 513.
21 John Clement, "Preconceptos de los estudiantes en mecánica introductoria" Revista estadounidense de física 50 (1982): 66 – 71.
22 Nella Grimellini Tomasini y Barbara Pecori Balandi, "Estrategias de enseñanza y ciencias de los niños: un experimento sobre la enseñanza sobre el" calor y el frío "" en Actas del segundo seminario internacional: conceptos erróneos y estrategias educativas en ciencias y matemáticas; Julio 26 – 29, 1987ed. Joseph D. Novak (Ithaca, NY: Universidad de Cornell, 1987), 2: 158 – 171.
23 HW Huang y YJ Chiu, "Modelos conceptuales de los estudiantes sobre la naturaleza y la propagación de la luz", en Actas del tercer seminario internacional sobre conceptos erróneos y estrategias educativas en ciencias y matemáticased. Joseph D. Novak (Ithaca, NY: Universidad de Cornell, 1993).
24 R. Prüm, “¿Cómo abordan los niños de 12 años los circuitos eléctricos simples? Un microestudio sobre procesos de aprendizaje ", en Aspectos de la comprensión de la electricidad: actas de un taller internacionaled. Reinders Duit, Walter Jung y Christoph von Rhöneck (Kiel, Alemania: Institut für die Pädagogik der Naturwissenschaften, 1985), 227 – 234.
25 Vanessa Kind, "Conocimiento del contenido pedagógico en la educación científica: perspectivas y potencial para el progreso" Estudios en Ciencias de la Educación 45 (2009): 169 – 204.
26 Hunter McEwan y Barry Bull, "La naturaleza pedagógica del conocimiento de la materia" Revista de investigación educativa estadounidense 28 (1991): 316 – 334.
27 El término "efecto Matthew" fue acuñado por el sociólogo Robert Merton en 1968 y Keith Stanovich lo adaptó a un modelo educativo en 1986. Ver Robert K. Merton, "El efecto Matthew en la ciencia" Ciencia: 159, no. 3810 (enero 5, 1968): 56 – 63; y Keith E. Stanovich, "Efectos de Matthew en la lectura: algunas consecuencias de las diferencias individuales en la adquisición de la alfabetización" Investigación de lectura trimestral 21 (1986): 360 – 407.
28 Marilyn Jager Adams, Comenzando a leer: pensando y aprendiendo sobre la impresión (Cambridge, MA: MIT Press, 1990).
[ilustraciones de James Yang]